This article will be shorter than the rest, but it will focus on the syllogism that we have used frequently in the previous articles. Today, we will cover very important rules that are necessary for a valid syllogism, so that you can inspect your own for faults. The valid syllogism has to conform to six rules. Some logicians, like Patrick Hurley, reduce them to five by incorporating the first rule into the definition of a syllogism. That, in my opinion, is the correct way to do it. But I wish to include it as a separate rule to highlight it and bring it to the front, especially since it is perniciously prone to logical errors. It is essential to discuss how these rules work, how they can be avoided, and understanding which formal fallacies we commit by not following these rules. I would advise the reader to grab a pencil and paper and start making his own syllogisms, since this is the best way to learn how to detect the errors, and think on the fly.
Rule #1. All three terms, the predicate, the middle, and the subject, have to mean a particular thing, and they should retain that same particular meaning throughout the syllogism.
It should go without saying, but it needs to be said anyway: If any term in the syllogism changes its meaning at least once, that is sufficient to render the syllogism invalid. It is easy for the errors to slip in when this happens, casting great doubt on the conclusion, no matter how well-substantiated the premises are. This illicit substitution can be exhibited in two ways. The first of which is the substitution of terms which denote different things, even if they shared the same lexical entry in the dictionary. This is the extensional fallacy. Consider this silly (AAA-1) example.
[A] Odd numbers differ from the numbers expected (in a given context);
[A] The number three (3) is an odd number;
[A] The number three differs from the numbers expected.
It is highly improbable that you will meet anyone who makes this mistake. But then again, consider this very same fallacy in political speech (EAE-1):
[E] They say that liberals just don’t support price controls, it goes against their core values. [A] But then come all those mainstream democrats, claiming they’re liberals. [E] I would expect those democrats would not support price controls, but they do!
Notice the slimy middle term here. In the first sense, liberal in the major premise means classical liberal, whereas in the second sense, liberal in the minor premise means American liberal (usually referring to democrats, leftists, and civil libertarians). The term is linguistically shared, but the meanings of both terms differ. The term has multiple denotations, which leads to the extensional fallacy. When the focus is rather on the term itself and not on the denotation, this error is called Fallacy of the Fourth Term. Both fallacies commit the same errors, and we distinguish between them based on how they are exhibited.
The other fallacy is, instead, intensional, since it errs on the connotations of the term. This is often called the masked man fallacy. The classical example is given about someone who does not even wear a mask:
I don’t know who Superman is,
But I know Clark Kent.
Therefore, Clark Kent is not Superman.
The fallacy can also be written in standard form (AEE-4), combined with an enthymeme (where one premise is assumed, and the other, presented):
[A] The Amanita Muscaria is classified as a toxic fungus, [E] but in that up-to-date toxic fungi catalogue, I couldn’t find the Fly Agaric. [E] So, evidently, the Fly Agaric is not the Amanita Muscaria (since one is toxic, and the other isn’t).
Fallacies from Rule #1: Illicit Substitution of Identicals; Fallacy of the Four Terms; the Extensional Fallacy; the Intensional (or Masked Man) Fallacy.
Rule #2. It is impermissible to draw a particular conclusion from two universal premises.
Since universal premises do not have universal import, but particular conclusions do, as we have explained above (article 2), then from the Boolean standpoint, this is considered a fallacy. We infer the existence of a term when none have been assumed to exist. Consider this unconditionally valid form (AEE4), but with the conclusion (E ↔ O):
[A] All apples are fruits;
[E] All fruits are not roots.
[O] Therefore, some roots are not apples.
Although the conclusion is sound, it does not follow from the premises in only the Boolean standpoint. (It does, from the Aristotelian standpoint if the subject — roots — existed.)
This rule rules out 2 x 2 x 2 x 4 = 32 syllogism (12.5% of 256, all possible syllogisms):
| AAI-X | EAI-X |
| AAO-X | EAO-X |
| AEI-X | EEI-X |
| AEO-X | EEO-X |
Fallacies from Rule #2: The Existential Fallacy.
Rule #3. The middle term must be distributed at least once.
The middle term can be distributed twice, but it cannot be undistributed. This brings us back to the four forms: Terms are distributed if they follow the negative copula (is not), or the universal quantifier (all). The green terms below are distributed, whereas the red terms are not.
A: All S are P.
E: All S are not P.
I: Some S are P.
O: Some S are not P.
Looking at table 1 from article 2, we may construct another table with the 4 x 4 x 4 = 64 invalid syllogisms (25%) that break rule 3:
| Figure 1 | IAX, IIX, OAX, OIX |
| Figure 2 | AAX, AIX, IAX, IIX |
| Figure 3 | IIX, IOX, OIX, IOX |
| Figure 4 | AIX, IIX, AOX, IOX |
If we consider the reason behind this rule, it is obvious to see that the middle term links both the major and minor terms. Consider figure 1 below.

If the middle term was never distributed, then there can always be counter-examples. Consider [1] from the figure above. If some S are M and some M are P, it does not follow that some S are P (or that some S are not P, since it can be the case that x2 is x4 and we may delete x1). As for [2] and [3], M is distributed in both cases. In both, we talk about all the elements of M, and therefore we can make categorical statements about S and P in relation to M.
Fallacies from Rule #3: The Undistributed Middle Fallacy.
Rule #4. The term that is not distributed in any premise cannot be distributed in the conclusion.
To understand this rule, look again at figure 1 [1,2]. If we have not distributed S, then it may be the case that we are talking about x1, x2, or both. Since we have not specified, it is illicit to draw any categorical conclusion. By distributing it in the conclusion, we will have more information about S in the conclusion than is contained in the premises.
Fallacies from Rule #4: The Illicit Major Fallacy; The Illicit Minor Fallacy.
Rule #5. No conclusion may be drawn from two premises of negative polarity.
Some examples that demonstrate the errors here are hilarious. Consider this one (EOO-1):
All horses are not vehicles;
Some cars are not horses;
Some cars are not vehicles.
It is obvious that the conclusion is wrong. But the error can be more precisely pinpointed: We cannot know how much of each S and P are shared. Consider this figure.
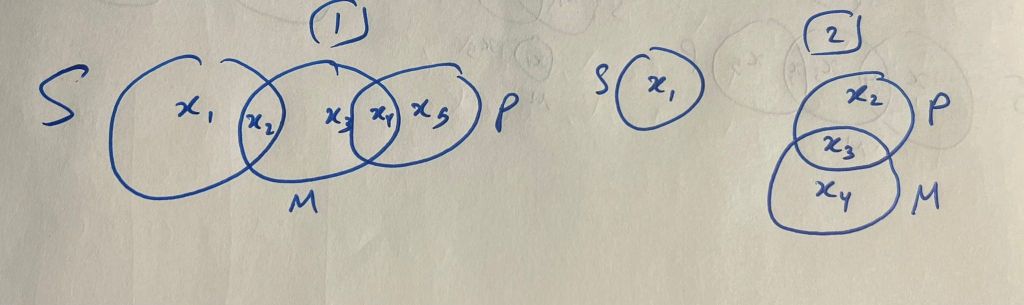
Consider then [1] from figure 2 again. Here’s another reason why Rule #3 is correct and works together with Rule #5. Suppose that ‘Some S are not M.’ We are saying that x1 is in S, but x1 is not in M. Further suppose that ‘Some P are not M.’ We may say now that x5 is in P, but it is not in M. Now, possible relations are that x1 is x5, or that x2, x3, and x4 are the same thing. We can infer nothing from this these negative statements. Now, we look at [2] from Figure 2 to focus on Rule #5. If ‘All S is not M,’ and ‘Some P is not M,’ we do not know if x1 is x2 or not.
This rule removes 2 x 2 x 4 x 4 = 64 (25%) of the syllogisms from the table from the previous article:
| EE-X | OE-X |
| EO-X | OO-X |
Fallacies from Rule #5: Fallacy of the Exclusive Premises.
Rule #6. The polarity of the conclusion follows from the polarity of the premises.
This rule says that if one of the premises has negative polarity (and it cannot be both, because of Rule #5), then the conclusion will have a negative polarity, and if all premises have positive polarity, then so shall the conclusion be of positive polarity. Consider this (AO I/O-4) syllogism:
All phones are electronic devices;
Some electronics are not waterproof;
Thus, some things that are waterproof are (are not) phones.
Notice that both conclusions are sound, but only the O and not the I, is valid. This is due to the fact that O follows from the premises, whereas I gives us more information not contained in them.
Fallacies from Rule #6: Drawing Affirmative/Negative Conclusions from Negative/Affirmative Premises.
Most of the material here was taken from section 3 of chapter 5 from Patrick Hurley’s textbook, A Concise Introduction to Logic, which I have used in my lecture notes. I have assigned that reading before class, and added examples of my own and incorporated some ideas from other sources to add to the discussion. Readers of Hurley’s book will notice that I have rearranged the rules based on what I would have liked to cover in order. I would recommend consulting the newest edition of the textbook. My edition was an old, used, instructor’s edition. It was still wonderful and in almost pristine shape, but I believe the edits in the newest edition makes it so much better. Thank you for reading. In the next article, we will be using the syllogism in professional writing.